1T 2025 vår LK20 LØSNING: Forskjell mellom sideversjoner
| (73 mellomliggende sideversjoner av samme bruker vises ikke) | |||
| Linje 31: | Linje 31: | ||
\[ x= -2 \vee x = 6 \] | \[ x= -2 \vee x = 6 \] | ||
\[ (x-6)(x+2) < 0 \] | |||
[[File:18062025-03.png|centre|400px]] | |||
\[ x \in <-2,6> \] | |||
====Oppgave 3==== | ====Oppgave 3==== | ||
$f(x) = ax^2 +bx + c$ | |||
Siden den skjærer i (0,9) er c = 9. | |||
Siden den har ett nullpunkt er $b^2- 4ac =0$ Dvs. $b^2 = 36a$ | |||
Velger a = 1 og får at b = -6 eller b = 6. | |||
Mulig funksjonsuttrykk: \[ f(x) = x^2+ 6x +9 \] | |||
(f har nullpunkt i -3 ) | |||
====Oppgave 4==== | ====Oppgave 4==== | ||
=====a)===== | |||
$x^3-7x^2-10x+16=0$ | |||
Dette er en tredjegradslikning, så vi prøver oss fram. Tester med x= 1: | |||
$1-7-10 +16 = 0$ | |||
x= 1 er en løsning. Vi utfører polynomdivisjon: | |||
[[File: 17062025-01.png|centre|300px]] | |||
$x^2-6x -16 = 0$ | |||
Vi bruker abc- formelen og får x= -2 eller x = 8. | |||
$L = \{- 2,1,8\}$ | |||
=====b)===== | |||
Vi ser at funksjonen har samme uttrykket som likningen i a. Da vet vi at enten passer B eller C. | |||
Vi deriverer og setter f'(0). Dersom svaret blir positivt, passer B. Blir det negativt passer C. | |||
$f'(x)= 3x^2-14x-10$ | |||
$f'(0) = -10$, altså passer grafen C. | |||
Ser også at f har et positivt konstantledd (16), som støtter graf C. | |||
====Oppgave 5==== | ====Oppgave 5==== | ||
=====a)===== | |||
[[File:17062025-02.png|centre|300px]] | |||
Alle vinkler er 60 grader. | |||
Normalen fra C på AB danner to 30, 60, 90 trekanter. | |||
\[Sin (30^{\circ}) = \frac{\frac 12 AB}{ AC} = \frac{1}{2} \] | |||
\[Cos (60^{\circ}) = \frac{\frac 12 AB}{ AC} = \frac{1}{2} \] | |||
=====b)===== | |||
[[File:18062025.png|centre|300px]] | |||
Bruker arealsetningen: | |||
\[ A= \frac 12 abSinC = \frac 12 \cdot 10 \cdot 6 \cdot \frac 12 = 15 \] | |||
=====c)===== | |||
[[File:18062025-01.png|centre|300px]] | |||
Bruker cosinussetningen: | |||
\[ QR^2 = 8^2+3^2-2\cdot 8 \cdot 3 \cdot \frac 12 \] | |||
\[ QR^2 =64 + 9 -24 \] | |||
\[ QR = 7 \] | |||
====Oppgave 6==== | ====Oppgave 6==== | ||
En matematisk identitet er en likning som alltid er sann, for alle verdier av den variable (innenfor definisjonsmengden). Høyresiden er identisk med venstresiden for alle verdier av variablen, derfor får man x=x i CAS. | |||
En likning som ikke er en identitet, er kun sann for spesifikke verdier av variabelen (løsninger). | |||
====Oppgave 7==== | ====Oppgave 7==== | ||
Programmet sjekker minimumsverdien til funksjonen $f(x) = x^2+2x - 15 $ i intervallet [ - 5,5]. | |||
Løkken, som starter på linje 7 i programmet, regner ut verdien til gitt x verdi og fortsetter med det så lenge y verdien (f(x)) er mindre enn den forrige. Når det ikke lengre er tilfellet skriver programmet ut "verdi", som er minimumsverdien til andregradsfunksjonen. | |||
Det som skrives ut er -16 | |||
\[ f'(x) = 2x+2 \] | |||
\[f'(x) = 0 \Rightarrow x =-1 \] | |||
\[f(-1) = -16 \] | |||
====DEL TO==== | |||
====Oppgave 1==== | |||
=====a)===== | |||
Utfører regresjonen og får K(x): | |||
[[File:19062025-03.png|400px|centre]] | |||
=====b)===== | |||
Stigningstallet er 70,2. Det betyr at antallet registrerte tilfeller i gjennomsnitt øker med 70,2 per måned, i perioden april 23 til september 24. | |||
=====c)===== | |||
5336, i følge modellen. | |||
====Oppgave 2==== | |||
x = antall store sekker | |||
y = antall små sekker | |||
[[File: 180622025-04.png|centre|300px]] | |||
Butikken solgte 48 store sekker og 32 små sekker. | |||
====Oppgave 3==== | |||
=====a)===== | |||
Alle trekantene er likebeinte, der de likebeinte sidene representerer radius i sirkelen. Det er 12 trekanter så arealet av en trekant er 10. Bruker arealsetningen: | |||
\[A = \frac 12 ab SinC \Rightarrow 10 = \frac 12 r^2 \frac 12 \Rightarrow r = \sqrt{40} \] | |||
\[ d= 2r = 2\sqrt {40} = 4 \sqrt{10}\] | |||
=====b)===== | |||
[[File: 21062025-03.png|centre|400px]] | |||
Vi multipliserer det positive svaret med 12 og får $24( \sqrt{15} - \sqrt 5)$ | |||
====Oppgave 4==== | |||
[[File: 18062025-05.png|400px]] | |||
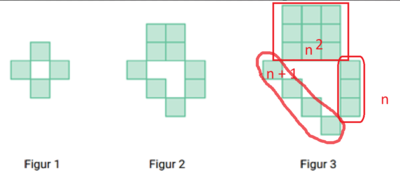
Antall kvadrater i figur nr. n er: $A(n) = n^2+n +(n+1) = n^2+2n+1 $ | |||
Eventuelt $A(n)=(n+1)^2$ | |||
=====a)===== | |||
* Lager en løkke som løper gjennom de 20 første figurene | |||
* Regner ut antall figurer på figur nr. n, ved å bruke formelen over | |||
* Skriver ut resultatet | |||
=====b)===== | |||
[[File:18062025-06.png|centre|400px]] | |||
Kolonne tre er ikke nødvendig i forhold til oppgaven, men det er jo greit å vite hvor mange kvadrater man bruke dersom man lager n figurer. Denne tellingen kommer fra linje 1 og 5. | |||
Vi får følgende ut: | |||
[[File:18062025-07.png|centre|100px]] | |||
Man trenger 441 kvadrater for å lage figur nr. 20. | |||
=====c)===== | |||
[[File:19062025-01.png|centre|300px]] | |||
[[File:19062025-02.png|centre|300px]] | |||
====Oppgave 5==== | |||
=====a)===== | |||
For å fylle inn tabellen trenger vi et uttrykk for høyden. Det er oppgitt at volumet skal være $450 cm^3$. | |||
\[ V = \pi r^2h \] | |||
\[ h = \frac{V}{\pi r^2} = \textcolor{red}{\frac{450}{\pi r^2}} \] | |||
[[File:21062025-01.png|centre|400px]] | |||
[[File:21062025-02.png|centre|400px]] | |||
=====b)===== | |||
Vi trenger et uttrykk for Overflate og radius: | |||
\[ O = \pi \cdot r^2 + 2 \cdot \pi \cdot r \cdot h \] | |||
Her har vi også variabelen h, men den kan vi erstatte med uttrykket fra a: | |||
\[ O = \pi \cdot r^2 + 2 \cdot \pi \cdot r \cdot \textcolor{red}{\frac{450}{\pi r^2}} \] | |||
\[ O(r) = \pi \cdot r^2 + \frac{900}{r } \] | |||
[[File:20062025-02.png|400px|centre]] | |||
=====c)===== | |||
Når radien er 5,23 cm oppnår man den minste overflaten, $257,97cm^2$. | |||
====Oppgave 6==== | |||
[[File:17062025-04.png|centre|400px]] | |||
*Nevneren må ha et uttrykk som gir to nullpunkter siden grafen på figuren har to bruddpunkt. | |||
*Grafen krysser y aksen på den positive side. Konstantleddene i teller og nevner er begge negative. Når x = 0 får man negativ delt på negativt, som er positivt. | |||
*Funksjonen har et nullpunkt for en positiv x verdi, i dette tilfellet når 5x-2=0, altså $x = \frac 25$. | |||
[[File:17062025-05.png|centre|400px]] | |||
*Nevneren kan ikke bli null. | |||
*Konstantleddene i teller og nevner utgjør en positiv brøk når x=0. | |||
Siste sideversjon per 21. jun. 2025 kl. 15:10
Diskusjon av oppgaven på Matteprat
Løsningsforslag laget av SveinR
Løsning fra OpenMathBooks prosjektet
DEL EN
Oppgave 1
\[f(x) = \frac{12x-3}{2x+1}\]
Vertikal asymptote : $2x+1 =0 \Rightarrow 2x =-1 \Rightarrow x= - \frac12 $
Horisontal asymptote: $y =\lim\limits_{x \to \infty} f(x)=\lim\limits_{x \to \infty} \frac{12x-3}{2x+1} =\lim\limits_{x \to \infty} \frac{\frac{12x}{x}- \frac{3}{x}}{\frac{2x}{x} + \frac {1}{x}} = \lim\limits_{x \to \infty} \frac{12- \frac{3}{x}}{2 + \frac {1}{x}} = 6$
Oppgave 2
\[x^2-4x-12<0 \]
Faktoriserer først uttrykket
\[x^2-4x-12=0 \]
\[x= \frac{4 \pm \sqrt{16+48}}{2} = \frac{4\pm 8}{2} \]
\[ x= -2 \vee x = 6 \]
\[ (x-6)(x+2) < 0 \]
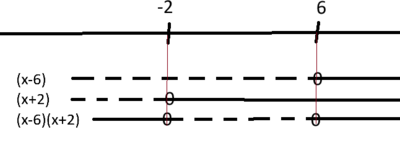
\[ x \in <-2,6> \]
Oppgave 3
$f(x) = ax^2 +bx + c$
Siden den skjærer i (0,9) er c = 9.
Siden den har ett nullpunkt er $b^2- 4ac =0$ Dvs. $b^2 = 36a$
Velger a = 1 og får at b = -6 eller b = 6.
Mulig funksjonsuttrykk: \[ f(x) = x^2+ 6x +9 \]
(f har nullpunkt i -3 )
Oppgave 4
a)
$x^3-7x^2-10x+16=0$
Dette er en tredjegradslikning, så vi prøver oss fram. Tester med x= 1:
$1-7-10 +16 = 0$
x= 1 er en løsning. Vi utfører polynomdivisjon:

$x^2-6x -16 = 0$
Vi bruker abc- formelen og får x= -2 eller x = 8.
$L = \{- 2,1,8\}$
b)
Vi ser at funksjonen har samme uttrykket som likningen i a. Da vet vi at enten passer B eller C.
Vi deriverer og setter f'(0). Dersom svaret blir positivt, passer B. Blir det negativt passer C.
$f'(x)= 3x^2-14x-10$
$f'(0) = -10$, altså passer grafen C.
Ser også at f har et positivt konstantledd (16), som støtter graf C.
Oppgave 5
a)
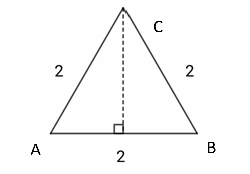
Alle vinkler er 60 grader.
Normalen fra C på AB danner to 30, 60, 90 trekanter.
\[Sin (30^{\circ}) = \frac{\frac 12 AB}{ AC} = \frac{1}{2} \]
\[Cos (60^{\circ}) = \frac{\frac 12 AB}{ AC} = \frac{1}{2} \]
b)
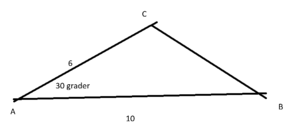
Bruker arealsetningen:
\[ A= \frac 12 abSinC = \frac 12 \cdot 10 \cdot 6 \cdot \frac 12 = 15 \]
c)
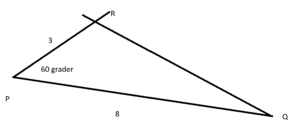
Bruker cosinussetningen:
\[ QR^2 = 8^2+3^2-2\cdot 8 \cdot 3 \cdot \frac 12 \] \[ QR^2 =64 + 9 -24 \] \[ QR = 7 \]
Oppgave 6
En matematisk identitet er en likning som alltid er sann, for alle verdier av den variable (innenfor definisjonsmengden). Høyresiden er identisk med venstresiden for alle verdier av variablen, derfor får man x=x i CAS.
En likning som ikke er en identitet, er kun sann for spesifikke verdier av variabelen (løsninger).
Oppgave 7
Programmet sjekker minimumsverdien til funksjonen $f(x) = x^2+2x - 15 $ i intervallet [ - 5,5].
Løkken, som starter på linje 7 i programmet, regner ut verdien til gitt x verdi og fortsetter med det så lenge y verdien (f(x)) er mindre enn den forrige. Når det ikke lengre er tilfellet skriver programmet ut "verdi", som er minimumsverdien til andregradsfunksjonen.
Det som skrives ut er -16
\[ f'(x) = 2x+2 \]
\[f'(x) = 0 \Rightarrow x =-1 \]
\[f(-1) = -16 \]
DEL TO
Oppgave 1
a)
Utfører regresjonen og får K(x):
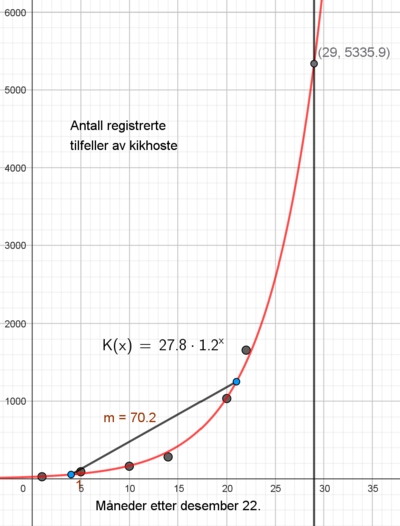
b)
Stigningstallet er 70,2. Det betyr at antallet registrerte tilfeller i gjennomsnitt øker med 70,2 per måned, i perioden april 23 til september 24.
c)
5336, i følge modellen.
Oppgave 2
x = antall store sekker
y = antall små sekker

Butikken solgte 48 store sekker og 32 små sekker.
Oppgave 3
a)
Alle trekantene er likebeinte, der de likebeinte sidene representerer radius i sirkelen. Det er 12 trekanter så arealet av en trekant er 10. Bruker arealsetningen:
\[A = \frac 12 ab SinC \Rightarrow 10 = \frac 12 r^2 \frac 12 \Rightarrow r = \sqrt{40} \] \[ d= 2r = 2\sqrt {40} = 4 \sqrt{10}\]
b)
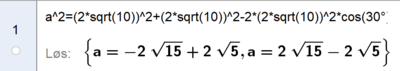
Vi multipliserer det positive svaret med 12 og får $24( \sqrt{15} - \sqrt 5)$
Oppgave 4
Antall kvadrater i figur nr. n er: $A(n) = n^2+n +(n+1) = n^2+2n+1 $
Eventuelt $A(n)=(n+1)^2$
a)
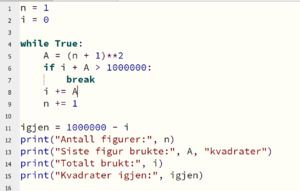
- Lager en løkke som løper gjennom de 20 første figurene
- Regner ut antall figurer på figur nr. n, ved å bruke formelen over
- Skriver ut resultatet
b)
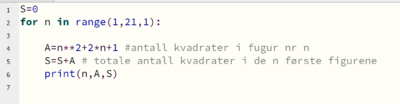
Kolonne tre er ikke nødvendig i forhold til oppgaven, men det er jo greit å vite hvor mange kvadrater man bruke dersom man lager n figurer. Denne tellingen kommer fra linje 1 og 5.
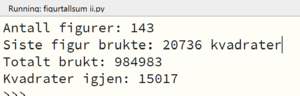
Vi får følgende ut:
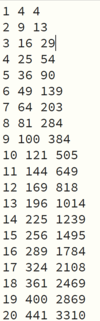
Man trenger 441 kvadrater for å lage figur nr. 20.
c)
Oppgave 5
a)
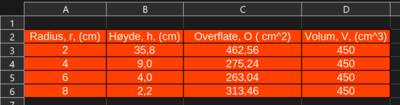
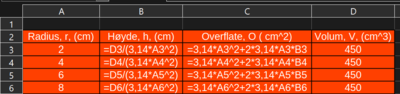
For å fylle inn tabellen trenger vi et uttrykk for høyden. Det er oppgitt at volumet skal være $450 cm^3$.
\[ V = \pi r^2h \] \[ h = \frac{V}{\pi r^2} = \textcolor{red}{\frac{450}{\pi r^2}} \]
b)
Vi trenger et uttrykk for Overflate og radius:
\[ O = \pi \cdot r^2 + 2 \cdot \pi \cdot r \cdot h \]
Her har vi også variabelen h, men den kan vi erstatte med uttrykket fra a:
\[ O = \pi \cdot r^2 + 2 \cdot \pi \cdot r \cdot \textcolor{red}{\frac{450}{\pi r^2}} \]
\[ O(r) = \pi \cdot r^2 + \frac{900}{r } \]
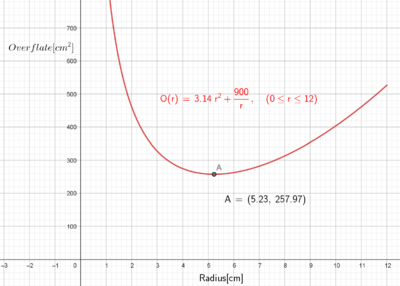
c)
Når radien er 5,23 cm oppnår man den minste overflaten, $257,97cm^2$.
Oppgave 6
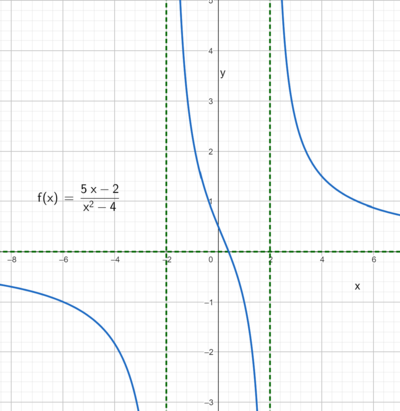
- Nevneren må ha et uttrykk som gir to nullpunkter siden grafen på figuren har to bruddpunkt.
- Grafen krysser y aksen på den positive side. Konstantleddene i teller og nevner er begge negative. Når x = 0 får man negativ delt på negativt, som er positivt.
- Funksjonen har et nullpunkt for en positiv x verdi, i dette tilfellet når 5x-2=0, altså $x = \frac 25$.
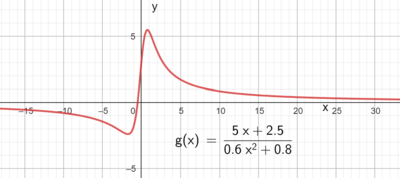
- Nevneren kan ikke bli null.
- Konstantleddene i teller og nevner utgjør en positiv brøk når x=0.