Andregradslikninger

Innledning

Fra siden om potenser vet vi at $x\cdot x=x^2$. Sagt med ord sier vi at "x multiplisert med seg selv er lik x i andre". Andregradsligninger inneholder alltid et ledd hvor $x^2$ er en faktor.

En annengradslikning er en likning på formen $a{x}^2+bx+c=0$, der a, b og c er konstanter og $a\ne 0$. Konstantene til en annengradslikning kalles koeffisienter.

En fullstendig andregradslikning skrives på formen $a{x}^2+bx+c=0$

• $a{x}^2$ kalles andregradsleddet
  
  
• $bx$ kalles førstegradsleddet
  
  
• $c$ kalles konstantleddet

Ufullstendig likning

Dersom a = 0 har vi en vanlig ligning som løses med metoden beskrevet i likninger med en ukjent.

Dersom b = 0 ser likningen slik ut:

$a{x}^2+c=0$

Denne løses med "bytt og flytt", for så å ta kvadratrot.
$x=\pm \sqrt{-\frac{c}{a}}$
Legg merke til at $a$ eller $c$ (men ikke begge!) må være negativ for at denne likningen skal ha en løsning. Ellers tar vi kvadratroten av et negativt tall.

Eksempel

$4x^2-8=0$


$x=\pm \sqrt{\frac{8}{4}}$

$x=\sqrt{2}\vee x=-\sqrt{2}$

Dersom c = 0 har vi følgende formel:

$a{x}^2+bx=0$

$x(ax+b)=0$

$x=0\vee ax+b=0$

$x=0\vee x=-\frac{b}{a}$

Eksempel:

$-3x^2+6x=0$

$x(-3x+6)=0$

$x=0\vee -3x+6=0$

$x=0\vee x=2$

Dette er spesialtilfeller av andregradslikninger fordi én av koeffisientene er lik null, slik at de mangler et ledd.

ABC formelen

En andregradslikning på formen $a{x}^2+bx+c=0$ kan alltid løses ved hjelp av ABC - formelen, som ser slik ut:

$x=\frac{-b\pm \sqrt{b^2-4ac}}{2a}$

når
$a{x}^2+bx+c=0$

Dersom $b^2-4ac$ er positiv vil likningen alltid ha to løsninger.

a, b og c er koefisienten i andregradsuttrykket. Legg merke til at dersom $b^2-4ac$ er mindre enn null får man et negativt tall under rottegnet. Man sier da at ligningen ikke har noen løsning. (I høyere kurs har den det, komplekse løsninger).

Eksempel 1
Vi har likningen:

$3x^2+2x-1=0$
a = 3 , b = 2 og c = -1
Ved å bruke abc-formelen får man:

$x=\frac{-2\pm \sqrt{2^2-4\cdot 3\cdot (-1)}}{2\cdot 3}$

$x=\frac{-2\pm \sqrt{4+12}}{6}$

$x=\frac{-2\pm 4}{6}$

$x=\frac{-2+4}{6}\vee x=\frac{-2-4}{6}$

$x=\frac{1}{3}\vee x=-1$

Eksempel 2
Vi har likningen:

$-x^2+4x-4=0$
a = -1 , b = 4 og c = -4
Ved å bruke abc-formelen får man:

$x=\frac{-4\pm \sqrt{4^2-4\cdot (-1)\cdot (-4)}}{2\cdot (-1)}$

$x=\frac{-4\pm \sqrt{16-16}}{-2}$

$x=2$
Med null under rottegnet får man kun en løsning.

Eksempel 3
Vi har likningen:

$3x^2+2x+2=0$
a = 1 , b = -2 og c = 2
Ved å bruke abc-formelen får man:

$x=\frac{2\pm \sqrt{(-2{)}^2-4\cdot 1\cdot 2}}{2\cdot 1}$

$x=\frac{2\pm \sqrt{4-8}}{2}$

$x=\frac{2\pm \sqrt{-4}}{2}$

Her ser man et man får et negativt tall under rottegnet. Da er det på tide å stoppe opp og konkludere med at ligningen ikke har løsning (enda).

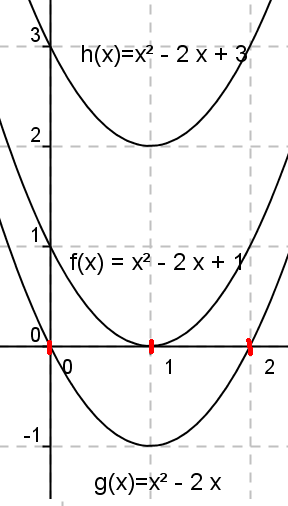
Hvorfor har noen likninger to løsninger, noen en og andre ingen?

Dersom grafen til andregradspolynomet krysser x aksen har likningen to løsninger, g(x).Dersom grafen tangerer x-aksen har likningen en løsning, f(x). Dersom grafen til polynomet ikke krysser eller tangerer x-aksen, h(x), har likningen ingen løsning.

Eksempel 4
Vi har likningen:

$4x^2-1=0$
a = 4 , b = 0 og c = -1
Ved å bruke abc-formelen får man:

$x=\frac{\pm \sqrt{-4\cdot 4\cdot (-1)}}{2\cdot 4}$

$x=\frac{\pm \sqrt{16}}{8}$

$x=\pm \frac{4}{8}$

$x=\frac{1}{2}\vee x=-\frac{1}{2}$

Her mangler b leddet og det er ikke nødvendig å bruke abc formelen slik vi har gjort her, men den virker. Det enkleste i dette eksempelet er å bruke "bytt og flytt" og så ta kvadratroten, som vist over.

Eksempel 5
Vi har likningen:

$-3x^2+6x=0$
a = -3 , b = 6 og c = 0
Ved å bruke abc-formelen får man:

$x=\frac{-6\pm \sqrt{6^2}}{-6}$

$x=\frac{-6\pm 6}{-6}$

$x=2\vee x=0$

Man ser at abc-formelen virker her også, men siden c leddet mangler ville det være mer fornuftig å faktorisere ut x og løse likningene som vist over.

For de som lurer på hvor abc-formelen kommer fra har man følgende bevis:

Bevis for ABC formelen:

$a{x}^2+bx+c=0$

$x^2+\frac{b}{a}x+\frac{c}{a}=0$

$x^2+\frac{b}{a}x=-\frac{c}{a}$

$x^2+2\frac{b}{2a}x=-\frac{c}{a}$

$x^2+2\frac{b}{2a}x+(\frac{b}{2a}{)}^2=-\frac{c}{a}+(\frac{b}{2a}{)}^2$

$(x+\frac{b}{2a}{)}^2=-\frac{c}{a}+\frac{b^2}{4a^2}$

$(x+\frac{b}{2a}{)}^2=-\frac{4ac}{4aa}+\frac{b^2}{4a^2}$

$(x+\frac{b}{2a}{)}^2=\frac{-4ac+b^2}{4a^2}$

$(x+\frac{b}{2a})=\sqrt{\frac{b^2-4ac}{4a^2}}\vee (x+\frac{b}{2a})=-\sqrt{\frac{b^2-4ac}{4a^2}}$

$x=-\frac{b}{2a}+\frac{\sqrt{b^2-4ac}}{2a}\vee x=-\frac{b}{2a}-\frac{\sqrt{b^2-4ac}}{2a}$

$x=\frac{-b+\sqrt{b^2-4ac}2a}{}\vee x=\frac{-b-\sqrt{b^2-4ac}}{2a}$

$x=\frac{-b\pm \sqrt{b^2-4ac}}{2a}$

Fullstendig kvadrat

Man kan bygge opp et fullstendig kvadrat ved å halvere, kvadrere, addere.....
For å kunne bruke teknikken må du kunne kvadratsetningene godt.
Her er hvordan det gjøres:

Eksempel
Vi har likningen:


$2x^2-3x+1=0$

$x^2-\frac{3}{2}x+\frac{1}{2}=0$

$x^2-\frac{3}{2}x=-\frac{1}{2}$

$x^2-\frac{3}{2}x=-\frac{1}{2}$

$x^2-\frac{3}{2}x+(\frac{3}{4}{)}^2=-\frac{1}{2}+(\frac{3}{4}{)}^2$

$(x-\frac{3}{4}{)}^2=\frac{1}{16}$

$x-\frac{3}{4}=\sqrt{\frac{1}{16}}\vee x-\frac{3}{4}=-\sqrt{\frac{1}{16}}$

$x=1\vee x=\frac{1}{2}$

Dersom du sliter med algebra bør du kanskje holde deg til abc-formelen, men dersom du har oversikt og har ambisjoner om femmere og seksere er metoden med fullstendig kvadrat noe du bør beherske.

Andregradsligninger på produktform

Man kan ha andregradsligninger på formen:

$(x+1)(x–2)=0$

Du ser at dette er en andregradsligning om du multiplisere ut parentesene:

$(x+1)(x–2)=x2-2x+x–2=x2–x–2$

Man kan multiplisere ut faktorene som vist over og bruke abc – formelen, men det finnes en mye enklere måte å løse ligningen på:

Dersom produktet av to faktorer skal bli null, må en av faktorene være null.

$mn=0$ medfører at $m$ eller $n$ må være lik null, om utsagnet skal være riktig.

I eksemplet

$(x+1)(x–2)=0$

betyr det at $x+1=0$ , eller at $x–2=0$

Det gir løsningene $x=-1$ V $x=2$

Problemet er redusert til løsninger av to enkle førstegradsligninger.

Faktorisering av andregradsuttrykk

$a{x}^2+bx+c$ er et generelt andregradsuttrykk. Ofte har man behov for å faktorisere uttrykket for å kunne forkorte og forenkle.

Man har følgende formel for faktorisering av andregradsuttrykk:

$a{x}^2+bx+c=a(x-x_1)(x-x_2)$

Der $x_1$ og $x_2$ er løsninger av $a{x}^2+bx+c=0$

Eksempel :
Faktoriser $6x^2-4x-2$

Løser først $6x^2-4x-2=0$ og får (abc – formelen)

$x_1=1\vee x_2=-\frac{1}{3}$

Bruker så formelen over og får:

$6x^2-4x-2=a(x-x_1)(x-x_2)=6(x-1)(x+\frac{1}{3})$

Dette er spesielt nyttig (helt nødvendig) når man skal forkorte brøker som inneholder andregradspolynomer.

Eksempel :

Sriv enklest mulig:

$\frac{6x^2-4x-2}{x+\frac{1}{3}}$

Faktorisere og får:

$\frac{6(x-1)(x+\frac{1}{3})}{x+\frac{1}{3}}=6(x-1)$

Sum og produkt av røtter

Man har følgende sammenhenger mellom sum og produkt av røtter (løsninger):

En fullstendig andregradslikning skrives på formen $a{x}^2+bx+c=0$

$x_1+x_2=-\frac{b}{a}$ og $x_1\cdot x_2=\frac{c}{a}$

der $x_1$ og $x_2$ er røtter (løsninger) i ligningen.

Eksempel

Vi ønsker å finne et andregradsutryk som har røttene x = -2 og x = 1.Utover det har vi ingen andre krav.

Vi får:
$x_1+x_2=-\frac{b}{a}$
$-2+1=-\frac{b}{a}$
$a=b$
Siden vi ikke har krav til koefisientene kan vi jo velge a = 1. Da får vi:
$a=1$
$b=1$

og $-2\cdot 1=\frac{c}{a}$
$c=-2$

Vi får da likningen

$x^2+x-2=0$

Ved å bruke abc-formelen ser man at dette er en (av mange) likninger som har løsning for x =1 og for x = -2.
Dersom man anvender disse formlene og finner en ligning må man sjekke at den virkelig har løsninger.

---

Tilbake til 1T Hovedside

Hovedside