Brøkregning
Brøk
| Hva er brøk? | Hvorfor brøk? | Å utvide brøk | Å forkorte brøk |
| Blandet tall | Addisjon / subtraksjon | Multiplikasjon / divisjon | Null i teller / nevner |
| Fra heltall til brøk |
Innledning
En brøk består av tre elementer: teller, brøkstrek og nevner.
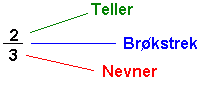
Brøkstreken betyr det samme som deletegn.
En brøk er en del av noe. Hvor stor del det er, avhenger av teller og nevner. Nevneren forteller hvor mange deler helheten er delt opp i.
Hvorfor trenger vi brøk?
En brøk kan angi en del av noe
Vi har tall som er mindre enn én enhet. En halv liter melk sier noe om mengden i forhold til enheten liter.
En brøk kan være svaret på et delestykke
<math>10 : 30 = \frac{10}{30} = \frac{1}{3}</math>
Kalkulator gir 0,33333…, som ikke er helt nøyaktig.
Tall større enn én kan også skrives som brøk:
<math>15 : 10 = \frac{15}{10} = \frac{3}{2}</math>
<math>\frac{3}{2} = 1,5</math>
Å utvide brøken
<math>\frac{1}{4} = \frac{2}{8} = \frac{4}{16}</math>
Vi multipliserer teller og nevner med samme tall.
Det er viktig at vi gjør det samme i teller og nevner.
Eksempel
<math>\frac{1}{4} = \frac{1 \cdot 2}{4 \cdot 2} = \frac{2}{8}</math>
Å forkorte brøken
Eksempel
<math>\frac{12}{16} = \frac{3}{4}</math>
Addisjon og subtraksjon
Lik nevner
<math>\frac{2}{7} + \frac{3}{7} = \frac{5}{7}</math>
<math>\frac{3}{5} - \frac{2}{5} = \frac{1}{5}</math>
Ulik nevner
<math>\frac{1}{3} + \frac{1}{2} = \frac{2}{6} + \frac{3}{6} = \frac{5}{6}</math>
Multiplikasjon
<math>\frac{2}{5} \cdot \frac{3}{4} = \frac{6}{20} = \frac{3}{10}</math>
Divisjon
<math>\frac{3}{4} : \frac{1}{2} = \frac{3}{2}</math>
Null i teller
<math>\frac{0}{n} = 0</math>, der <math>n \neq 0</math>
Null i nevner
Det er ikke mulig å ha null i nevner.
Teller og nevner like store
<math>\frac{n}{n} = 1</math>, der <math>n \neq 0</math>
Fra heltall til brøk
Et heltall kan skrives som brøk:
<math>4 = \frac{4}{1} = \frac{8}{2} = \frac{12}{3}</math>